Addition

The flowchart at the right describes the Number Class addition algorithm, and the diagram below illustrates the detailed steps for a specific example.

First the decimal points are aligned by increasing the lesser number's exponent and logically shifting its mantissa to the right by the corresponding number of digits.  In the actual implementation, for the sake of efficiency, a byte offset is maintained to avoid physically shifting by whole bytes.  If the difference in exponents is odd, an additional single-digit physical shift is performed on the lesser number.

As with all of the Number Class algorithms, the actual computation is performed in units of bytes, i.e. processing two decimal digits at a time from each of the operands.  The addition is performed starting from the rightmost end, and the bytes are added with carry, if any.  If there is a carry at the leftmost end, then the result exponent is incremented by one, and a single-digit shift is applied to remove the leading zero.  Finally, any trailing zero bytes are removed, and rounding is done if the result's scale exceeds the scale of the number being operated upon.

In the illustration below, unbiased byte values are shown for clarity, however the actual implementation operates directly upon the biased values of the Number Class internal representation.

Subtraction

The flowchart at the right describes the Number Class subtraction algorithm, and the diagram below illustrates the detailed steps for a specific example.

First the decimal points are aligned by increasing the lesser (in absolute value) number's exponent and logically shifting its mantissa to the right by the corresponding number of digits.  In the actual implementation, for the sake of efficiency, a byte offset is maintained to avoid physically shifting by whole bytes.  If the difference in exponents is odd, an additional single-digit physical shift is performed on the lesser number.

As with all of the Number Class algorithms, the actual computation is performed in units of bytes, i.e. processing two decimal digits at a time from each of the operands.  The subtraction is performed starting from the rightmost end, and the bytes are subtracted with carry, if any.  Since the lesser number is always subtracted from the greater, there is never a carry beyond the leftmost digit.  Any leading zero digits are removed by logically shifting the mantissa leftward and correspondingly decrementing the result's exponent.  Finally, any trailing zero bytes are removed, and rounding is done if the result's scale exceeds the scale of the number being operated upon.

In the illustration below, unbiased byte values are shown for clarity, however the actual implementation operates directly upon the biased values of the Number Class internal representation.

Multiplication

The flowchart at the right describes the Number Class multiplication algorithm, and the diagram below illustrates the detailed steps for a specific example.

First the result's sign, maximum length, and tentative exponent are determined, and an buffer of sufficient size is allocated and initialized with zeroes.  This buffer is used to accumulate the results of each loop cycle with the un-biased result bytes.  The proper bias required by the Number Class internal representation is applied to the result as a final step.

For efficiency, the outer loop ranges over the mantissa bytes of the shorter operand, from right to left.  The inner loop performs a multiplication on the next pair of un-biased bytes values and adds this result to the next result accumulator byte, again processing from right to left.  With each successive outer loop cycle the offset of the lowest order (rightmost) result byte computed moves leftward by one byte.

Trailing zeroes are always removed, except at most a final zero digit if needed to fill out the last full byte.  If the final result accumulator contains a leading zero, this is removed by shifting the mantissa left by a single digit.  Otherwise, the tentative exponent is incremented, and the exponent's final sign and bias are applied.  Rounding is done if the result's scale exceeds the scale of the number being operated upon.

In the illustration below, unbiased byte values are shown (in black) for clarity, however the actual implementation operates directly upon the biased operand values.  The accumulator (in green) holds un-biased byte values while processing is being performed.

Division

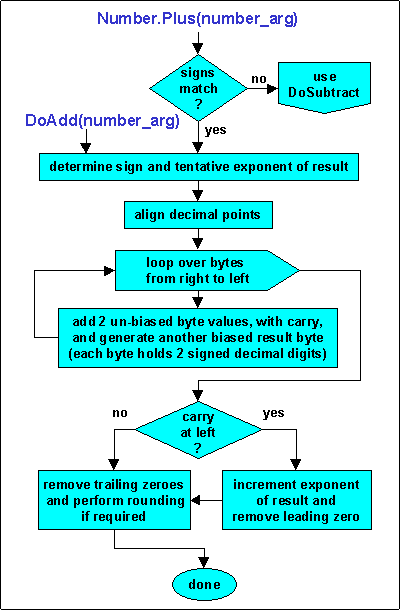
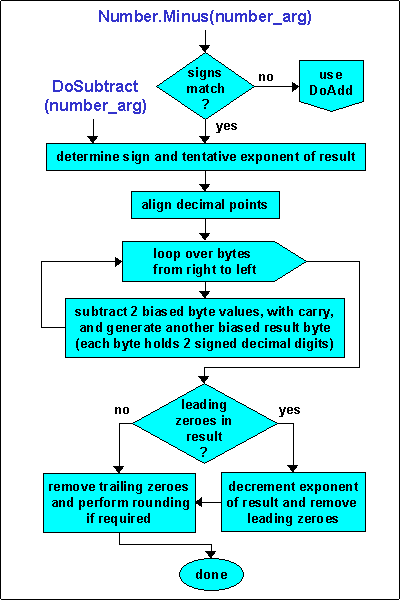
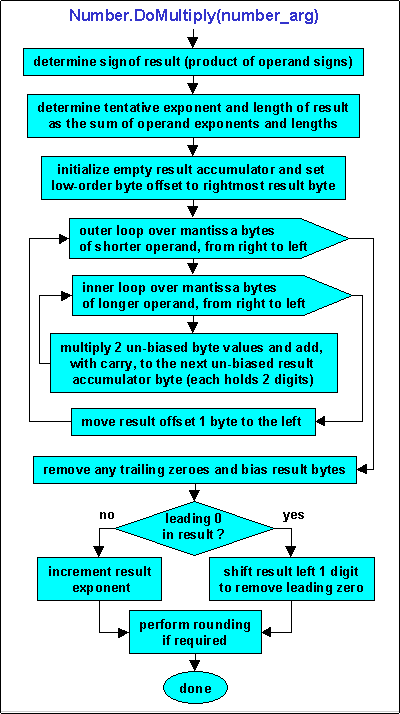
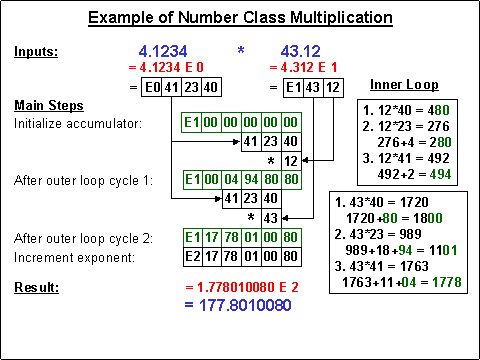
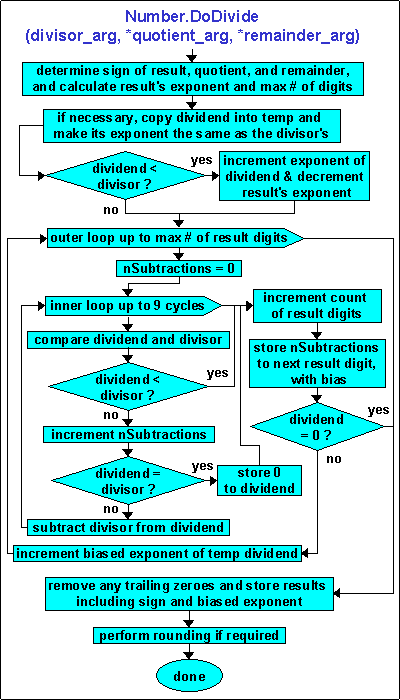
The flowchart at the right describes the Number Class division algorithm, and the diagram below illustrates the detailed steps for a specific example.  DoDivide supports either division or a quotient and/or remainder function, depending on whether non-null arguments are supplied.  For the quotient and remainder cases, the logic will generally terminate sooner than for a full division; this diagram only shows the details of the division case.

First the signs of the result, quotient, and remainder are determined.  The result's (and quotient's) sign is positive if both the operands have same sign, otherwise it is negative, and the sign of the remainder is always that of the dividend, i.e. the number being operated upon.  The result's exponent is calculated as the difference of the exponents of the dividend and the divisor argument.  A maximum number of result mantissa digits is calculated by adding the result's exponent, plus an allowance for the Number Class variable's declared scale factor (i.e. digits to be retained to the right of the decimal point), plus an extra digit to support proper rounding to the desired scale.

A result accumulator of sufficient length is allocated and the dividend is copied into this temporary Number Class variable, which will be used as the remaining dividend in the following logic.  (For the special case of a quotient/remainder operation, however, the calculation immediately finishes at this point if the divisor is larger than the dividend.)  The exponent of the temporary dividend is then adjusted to be the same as that of the divisor.  If  this leaves the dividend smaller than the divisor, the dividend's exponent is incremented and the result's exponent is decremented, as the final initialization step.

The main loop generates one mantissa digit on each cycle, filling the result accumulator from left to right.  Each result digit is computed by an inner loop that subtracts the divisor from the dividend, until the remaining dividend is less than (in absolute value) the divisor.  Note that these comparison and subtraction operations are performed via Number Class functions, CompAbsVal and DoSubtract, since the divisor and dividend are both Number Class objects.  The number of subtractions performed by the inner loop yields the next digit of the result.  If the remainder is zero, the outer loop terminates; otherwise the remaining dividend is multiplied by 10 and processing for the next result digit continues, up to the required scale and precision.  (If obtaining only quotient/remainder, exit when we have calculated all the result digits to the left of the decimal point, i.e. the quotient.)

Trailing zeroes are always removed, except at most a last zero digit if needed to fill out the last full byte.  A final rounding step is done only if the result's scale exceeds the scale of the number being operated upon.

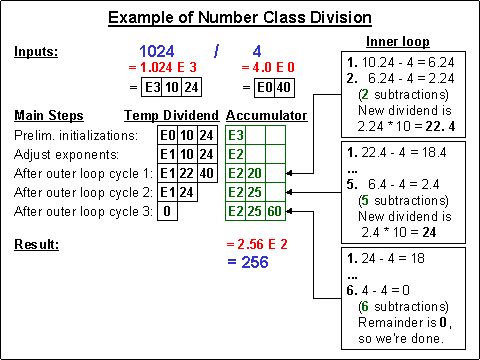
In the illustration below, unbiased byte values are shown (in black) for clarity, however the actual implementation operates directly upon biased Number Class values in their standard internal representation.  The accumulator (in green) is generated with biased mantissa bytes as each result digit is obtained.  Note that this example illustrates an instance where the initial temporary dividend (1.024), after forcing its exponent to that of the divisor (0), is smaller than the divisor (4.0), so the dividend's exponent is incremented and the result's exponent is decremented.  Thus the outer loop logic begins its processing against a dividend of 10.24.

Copyright © 2012, Base One International Corporation